Nell’articolo di ieri abbiamo spiegato come costruire quadrati di Gann di minimo e massimo in scala 2 e 3.
Ma esiste un altro tipo di quadrato, quello di range.
Il range altro non è che la differenza di prezzo tra un minimo ed un massimo o tra un massimo ed un minimo.
Altro elemento rilevante il numero di unità temporali intercorrenti tra i due estremi.
Come costruire quadrati di range in scala 2 e 3
Per costruire, quindi, un quadrato di range in scala 2 e 3 si procede nello stesso modo, già considerato per i quadrati di min/max.
Unica differenza consiste nel partire dal range, invece che dal valore di minimo/massimo.
Esempio: quadrato di range in scala 3 su euro dollaro
Consideriamo, sull’Euro dollaro, il range compreso tra luglio 2008 e gennaio 2017, con time frame mensile.
Il range è pari a 1,603 – 1,0339, da cui otteniamo 0,5697.
La distanza temporale è di 102 barre mensili.
Di qui otteniamo un primo valore della retta 1X1, pari a: 0,5697/102, da cui ricaviamo il valore di 0,0058.
Ora procediamo a dividere il numero 1 per 3, tante volte, fin tanto che troviamo un valore che approssima 0,0058.
Quindi 1/3/3/3/3/3, da cui ricaviamo 0,004115. Questo il nuovo valore della 1X1.
Non resta, infine, che dividere il range per questo nuovo valore, da cui: 0,5697/0,004115, ricavando il valore di 138 unità mensili.
Applicando graficamente otteniamo quanto segue.
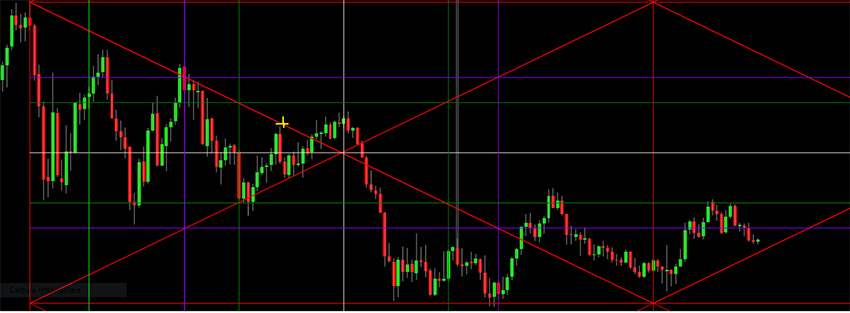
Notiamo che i riferimenti grafici entro il quadrato, costituiti da setup (rette verticali), vettori angolari e ritracciamenti orizzontali, colgono alcune indicazioni tecniche di rilievo.
In particolare, su diversi setup assistiamo a punti di svolta del trend.
Parimenti, i livelli statici svolgono egregiamente funzione di supporto e resistenza.
Ed analoga funzione svolgono i vettori angolari.
A cura di Gian Piero Turletti, autore di “Magic Box” e “PLT“





