Avevamo già trattato in precedenti occasioni alcuni temi relativi a molteplici tecniche di analisi, comprese quelle di Gann. In particolare in un articolo, avevamo spiegato come costruire i quadrati di minimo e di massimo di Gann.
Oggi riprendiamo questo tema, ma approfondendo una diversa tecnica nella costruzione dei quadrati.
Come noto, infatti, esistono diverse modalità, per applicare certe tecniche, ed oggi vediamo la seguente.
Come costruire quadrati di Gann in scala 2 e 3
Occorre premettere che tale tecnica può applicarsi sia ai quadrati di minimo e di massimo, che ai quadrati di range.
Procediamo quindi nelle spiegazioni, partendo dal primo tipo di quadrato, ossia quelli di minimo e di massimo.
Si parte dalla quotazione di un minimo o di un massimo rilevante.
Quindi si divide tale prezzo per uno dei cicli temporali, ritenuti rilevanti da Gann, tipicamente 360 o sottomultipli di questo numero, e si segna il risultato.
A questo punto, se il risultato è superiore ad 1, si moltiplica il numero 1 tante volte per 2 (scala 2) o per 3 (scala 3), fino ad ottenere il risultato più vicino a quello ottenuto in base alla divisione del prezzo per 360 (o sottomultipli).
Se il risultato della divisione per 360, o sottomultipli, è invece inferiore ad 1, si divide per 2 o per 3, invece di moltiplicare, ricercando sempre il risultato che maggiormente si avvicina alla divisione del prezzo per 360 (o suoi sottomultipli).
Abbiamo così ottenuto il valore della 1×1.
Come ultimo passaggio, non resta che nuovamente dividere il prezzo di minimo o massimo, da cui siamo partiti, per il valore della 1×1, e troviamo così il numero di unità temporali, su cui costruire il nostro quadrato.
Ancora una volta risulta più facile farlo, che spiegarlo.
Esempi
Presentiamo due esempi.
Il primo, relativo all’euro dollaro su time frame mensile, si riferisce alla costruzione di un quadrato di massimo in scala 2.
Il secondo, sempre su time frame mensile, è relativo ad un quadrato di minimo in scala 3 sull’oro.
Euro dollaro: quadrato di massimo in scala 2
Partiamo dal massimo del mese di luglio 2008 a 1,6036 e lo dividiamo per 360, ottenendo 0,0044, risultato inferiore ad 1.
Quindi dividiamo 1 per 2 diverse volte, in quanto intendiamo costruire un quadrato in scala 2, fin tanto che otteniamo il risultato più vicino a 0,0044.
Ossia: 1/2/2/2/2/2/2/2/2, che abbreviato possiamo scrivere come 2^-8, ossia 1 diviso 2 elevato alla ottava.
Il risultato che troviamo è 0,0039, che è quello che approssima 0,0044, di cui sopra.
Infine: 1,6036/0,0044, da cui ricaviamo 364,45, che possiamo arrotondare a 364.
Applicando, il risultato grafico è il seguente.
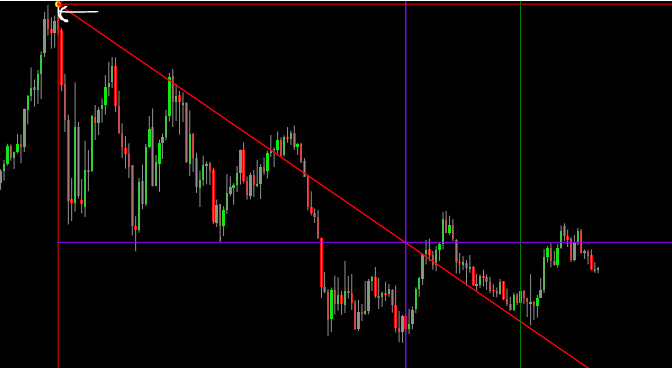
La freccia bianca in alto a sinistra indica il massimo di partenza.
La retta orizzontale blu si riferisce ad un livello di prezzo, di cui si nota la rilevanza.
La retta rossa indica un vettore angolare discendente, che intercetta buona parte dei prezzi.
Mentre le rette verticali indicano setup temporali, altrettanto importanti.
Oro in dollari: quadrato di minimo in scala 3
Partiamo dal minimo di dicembre 2015 a 1.045,85.
Quindi: 1.045,85/360 porta a 2,9.
Si tratta di risultato superiore ad 1, quindi moltiplichiamo.
Il risultato, moltiplicando per 3, più vicino a 2,9, è 3. In quanto intendiamo costruire un quadrato in scala 3.
Quindi 3 rappresenta la nostra 1×1, ed infine: 1.045,85/3 porta ad un risultato di 348,61, che possiamo arrotondare a 349, il numero delle unità temporali.
Applicando i parametri, sopra trovati, risulta il seguente grafico.
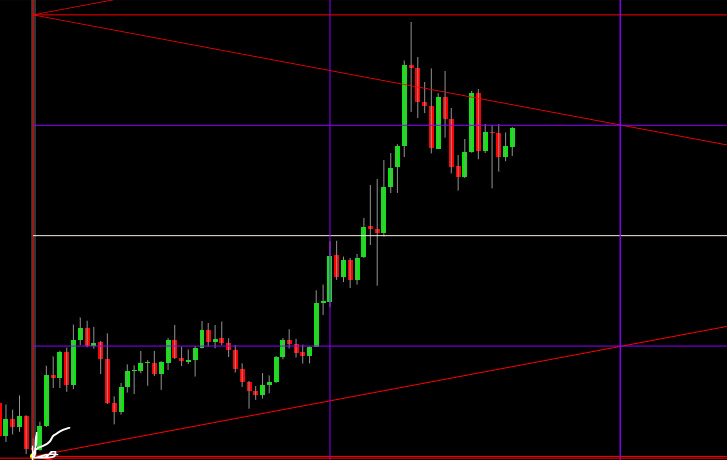
La freccia bianca in basso a sinistra indica il minimo di partenza.
Le rette verticali indicano setup temporali (da notare che in coincidenza con quella presente sui prezzi il trend ha interrotto il proprio trend ascendente, lateralizzando).
In rosso vettori angolari che approssimano bene i trend in atto. Infine, le rette orizzontali blu hanno colto livelli di prezzo di supporto/resistenza.
Per concludere su come costruire quadrati di Gann in scala 2 e 3, anticipo che in un successivo articolo vedremo come usare la stessa tecnica, ma per costruire quadrati cosiddetti di range.
A cura di Gian Piero Turletti, autore di “Magic Box” e “PLT“





